
This page presents some of the interfacial trajectories (i.e. fronts) between stationary states with periodic pattern that appear in (discrete) bistable reaction-diffusion systems. The dynamics is generated by the following recursion:
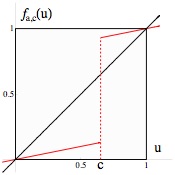
where is a piecewise affine bistable real map.
Parameter ranges:
The existence of fronts and their velocity depend on parameters. In addition, these solutions are asymptotically stable and robust with respect to small perturbations of the dynamics, see A31 or video and slides of the IMA ’12 talk, for more details.
Fronts between periodic patterns
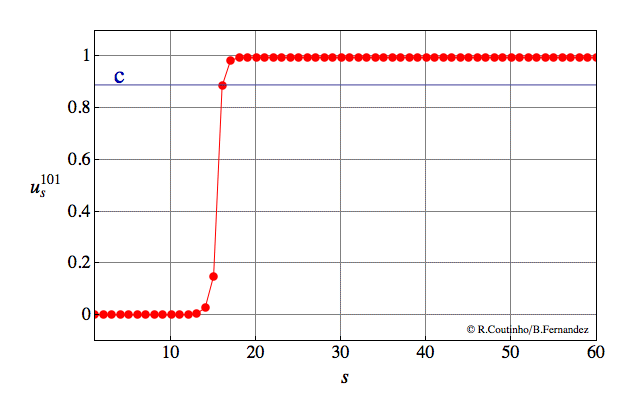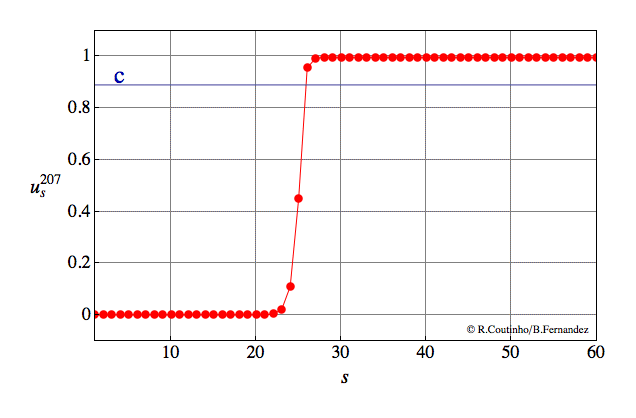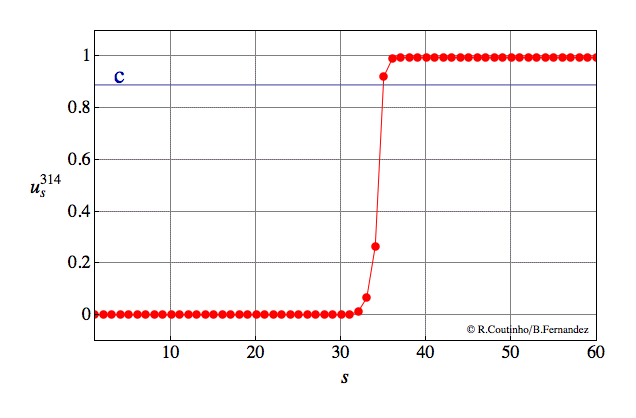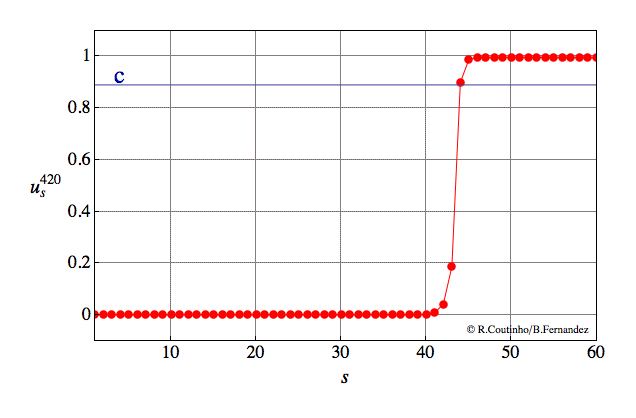
Standard front
i.e. invasion phenomenon of a stationary state with constant pattern as a pure traveling wave.
Parameter values:
a=0.8
ε = 0.07
c = 0.9
v = 2/23
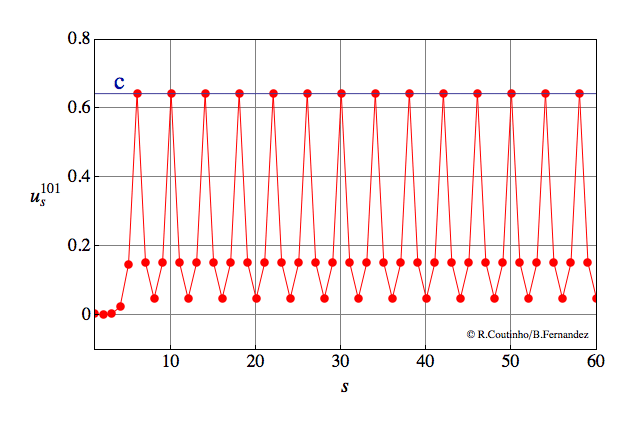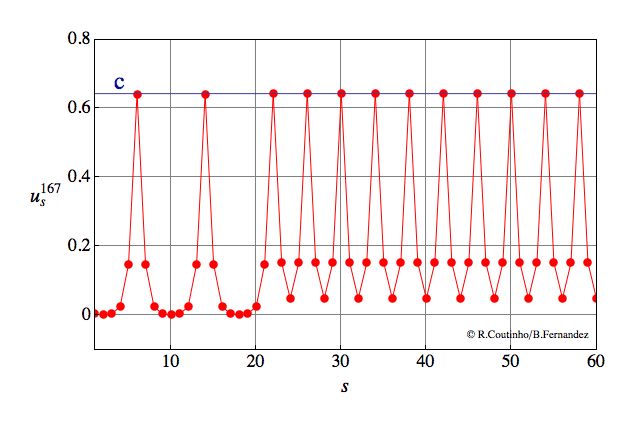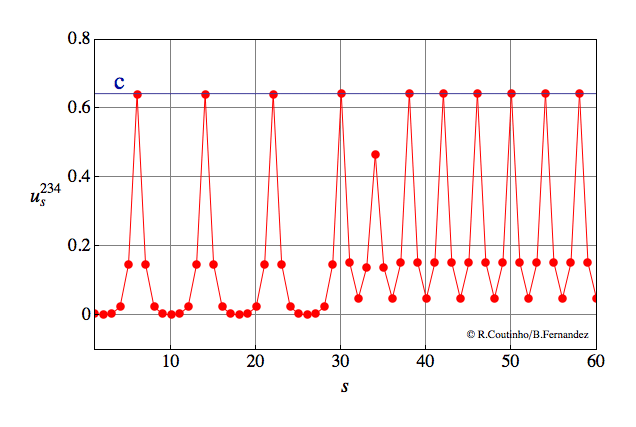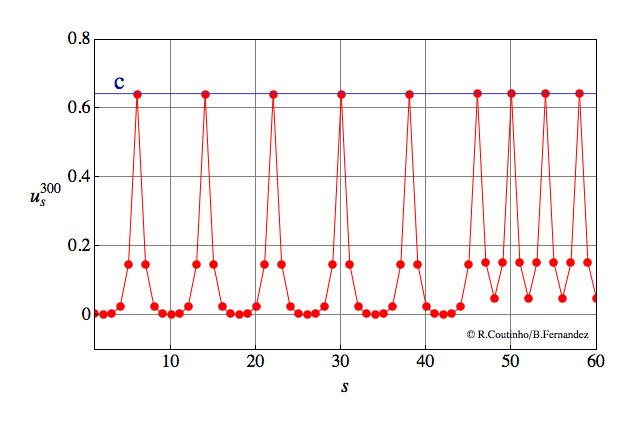
Front into a periodic pattern
Invasion of a state with 2-periodic profile.
Parameter values
a=0.8
ε = 0.07
c = 0.762
v = 2/23
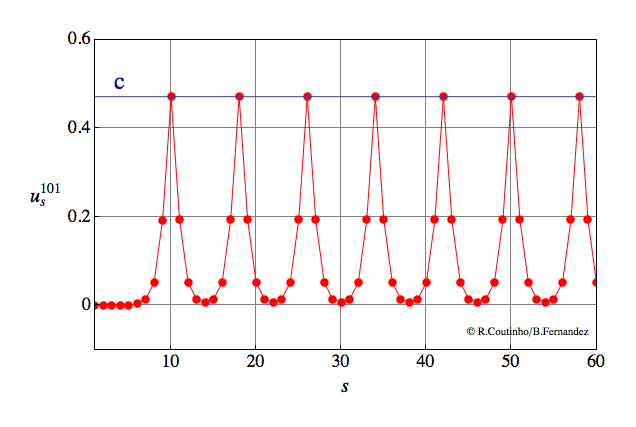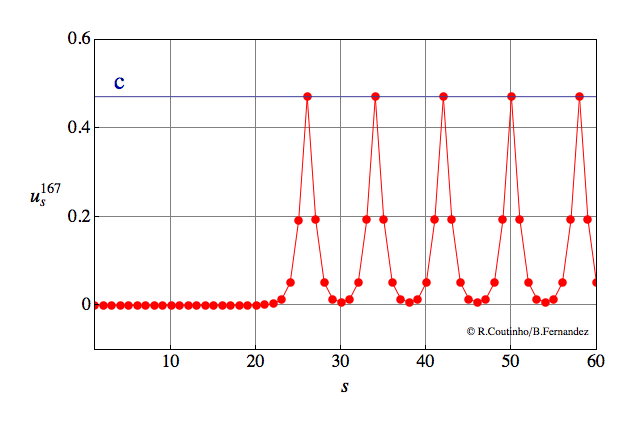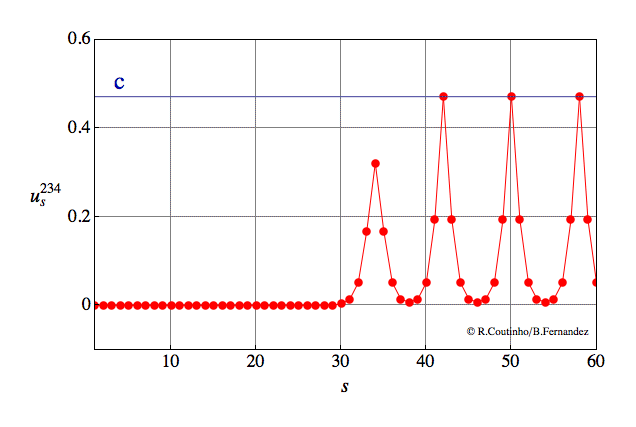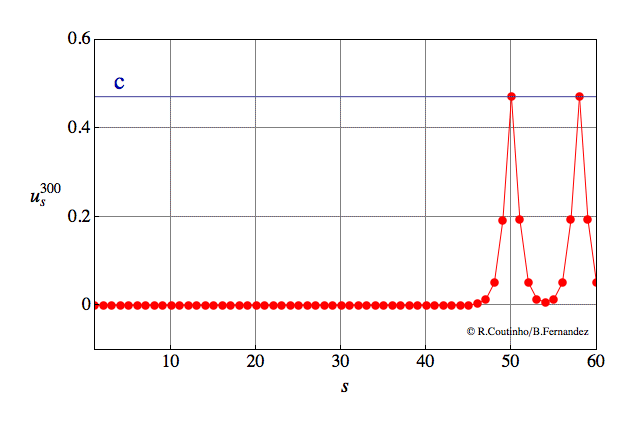
Front into a periodic pattern (2)
Invasion of a state with 8-periodic profile.
Parameter values
a=0.8
ε = 0.25
c = 0.471
v = 2/11
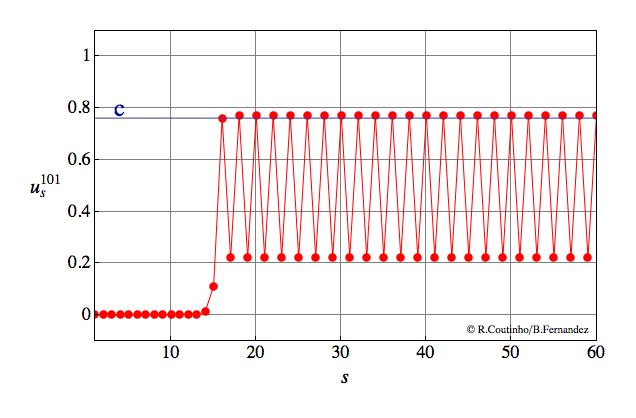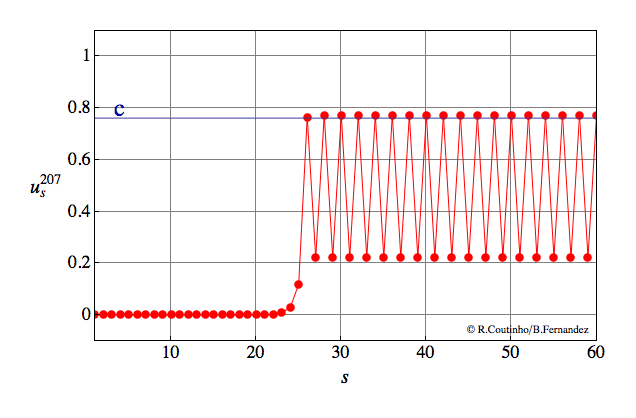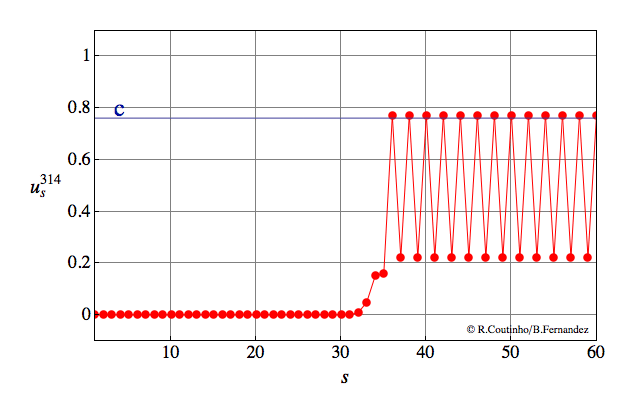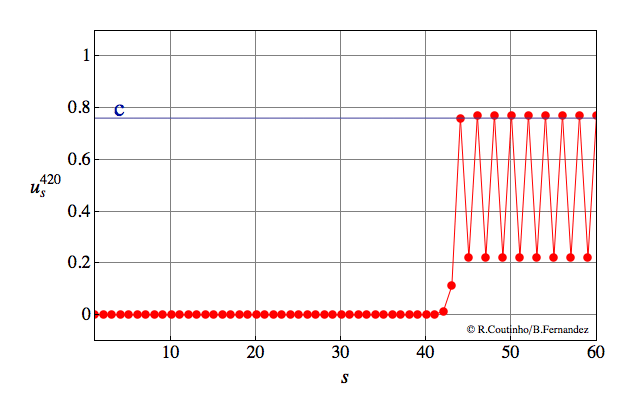
Front between two periodic patterns
Invasion of a state with 4-periodic profile by a state with 8-periodic profile.
Parameter values
a=0.8
ε = 0.12
c = 0.643
v = 2/11
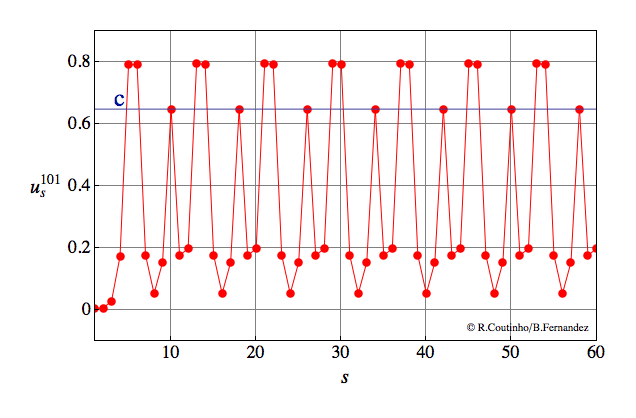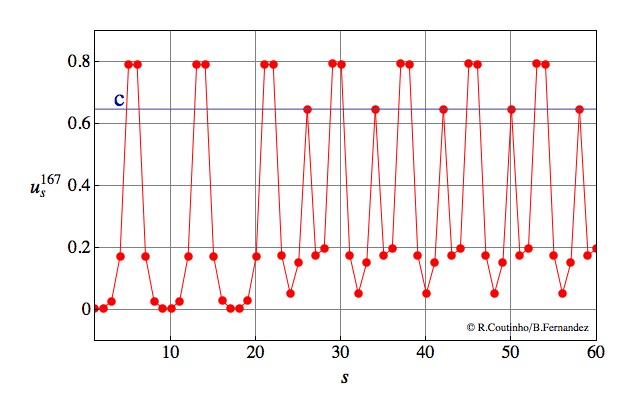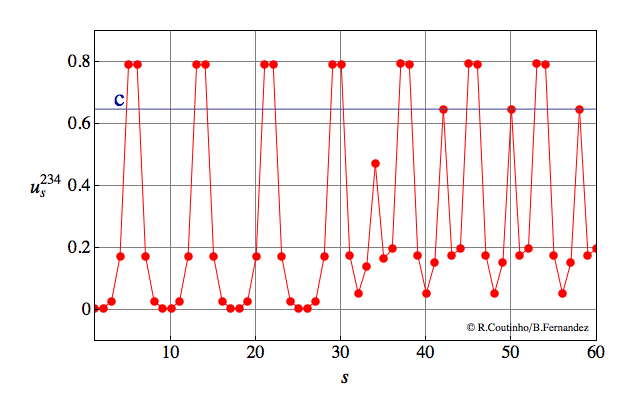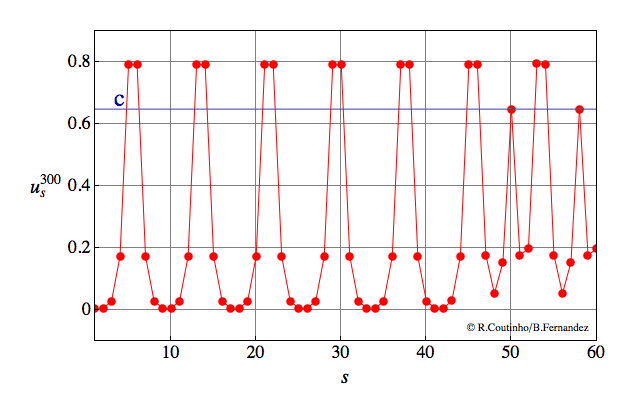
Front between two periodic patterns (2)
Invasion of a state with 8-periodic profile by another state with 8-periodic profile.
Parameter values
a=0.8
ε = 0.12
c = 0.647
v = 2/11
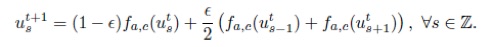
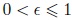
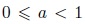
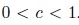

here:






V. Hirbec
V. Hirbec